|
个人信息Personal Information
教授
硕士生导师
教师拼音名称：Liang Yingzong
入职时间：2018-12-27
所在单位：材料与能源学院
联系方式：yliang@gdut.edu.cn
在职信息：在职
主要任职：Professor
其他任职：Professor
毕业院校：The Hong Kong University of Technology
学科：工程热物理
博弈论
点击次数：
简介
博弈论 (Game Theory) 是数学的一个分支，用于分析和预测具有不同数量玩家的多种不同游戏场景的趋势。博弈论的应用可以在许多学科中找到，包括经济学、生物学、政治学、计算机系统和哲学。[1]
Emile Borel 被认为是 1921 年第一位提出正式博弈论的数学家，但博弈论的流行在 1944 年约翰·冯·诺伊曼和奥斯卡·摩根斯特恩发表了《博弈论与经济行为》后变得更加明显。在20世纪50年代和1960年代，博弈论应用扩展到战争、政治、哲学以及政治和社会科学。[1]
一般来说，游戏分为两大类：非合作游戏和合作游戏。在这两个类别中，存在许多不同的游戏类型。非合作博弈被定义为“每个参与者独立行动，不与其他人合作，并选择提高自己利益的策略”的博弈，而合作博弈被定义为“一组参与者寻求形成合作群体以提高自身利益的博弈”。他们在竞技游戏中的表现，并使玩家能够成功实现他们可能无法独立完成的目标”。[1]
最优选择及其对博弈的相对影响可以通过博弈论中的数学方法进行分析。然而，可能的组合数量随着玩家数量呈指数增长，因此最优解决方案可能并不总是计算上现实的可能性。本文旨在讨论 GT 的理论和方法，提供数值例子，并讨论博弈论的应用。[1]
理论
纳什均衡是博弈论中的一个基本概念。它最广泛地用于预测社会科学中战略互动的结果。游戏由以下部分组成：一组玩家、每个玩家可用的一组动作以及每个玩家的收益函数。收益函数是玩家对动作配置文件的偏好。“纯策略纳什均衡”是一种行动配置文件，其属性是任何单个参与者都无法通过偏离该配置文件来获得更高的收益。[3]
经典的囚徒困境博弈被广泛用来证明纳什均衡。在这个决策游戏中，如果一个玩家在另一个玩家说话时保持沉默，该玩家将被判入狱 10 年。如果他们都开口说话，他们都会被判 8 年徒刑。如果都不说话，他们都将被判两年徒刑。这个游戏的纳什均衡是每个玩家都说话并得到 8 年。虽然两个玩家都保持沉默是最佳解决方案，但两个玩家都没有动力偏离这一配置，因为保持沉默的玩家处境更糟。[2]
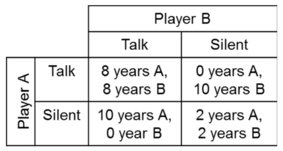囚徒困境游戏中两名玩家的收益。[2]
方法
纳什均衡通常用作描述涉及两个或更多人的非合作博弈的例子。混合整数线性规划 (MILP) 是一种优化方法，旨在在给定至少一个约束的情况下最大化或最小化线性目标函数。此外，MILP 问题中的一些变量是离散的，而其他变量是连续的。纳什均衡可以通过混合整数线性规划优化找到。还可以使用其他优化方法找到它，例如 Tsaknakis 和 Spirakis 创建的方法。他们的方法采用了玩家的收益与其他玩家根据他们选择的策略可以实现的最佳收益的最大偏差。[4]
线性规划 (LP) 是优化中使用的另一种方法，用于描述具有线性和连续的目标函数、约束和变量的问题。它可用于确定石头剪刀布等简单游戏或更复杂的扑克游戏的最佳策略。[5]该目标类似于 MILP 问题，因为它量化决策结果以实现特定结果。[6]对于涉及两个玩家的石头剪刀布游戏，一个玩家的选项集定义为 a，其中 a = {1, 2, 3}，另一个玩家的选项集定义为 b，其中 b = {1 、2 和 3}。每个玩家可以从三个选项之一中做出选择，即摇滚，由数字 1 代表，依此类推。他们的选择导致获胜、失败或平局，收益分别由 1、-1 或 0 表示。根据已确定的玩游戏的次数，可以生成一个矩阵来对双方玩家做出的决策集的结果和大小进行建模。
算法
与计算纳什均衡相关的常见算法是 Lemke-Howson 算法。该算法利用迭代旋转，与线性规划中使用的单纯形算法非常相似。两种算法之间的显着区别在于，与单纯形算法不同，Lemke-Howson 算法无法在多项式时间内运行。Lemke-Howson 算法可以被认为是一种强力算法，其中我们利用可能的解决方案作为猜测，并通过每次迭代继续调整它，直到达到纳什均衡。[4]
莱姆克·豪森枢轴行走
tableau 方法是一个枢轴过程，可用于使用 Lemke-Howson 算法找到纳什均衡。第一步是预处理，这里的目标是通过迭代来维持主导策略来限制游戏的选项。这降低了问题的复杂性，从而减少了解决问题所需的工作量。下一步是表格的初始化。游戏中的每个玩家都需要一张画面。现在，有了构建好的画面，我们就可以开始旋转了。这里的主要方面是入口和出口变量。退出变量是下一个主元的入口变量，直到满足互补条件。[4]
该算法流程由四个主要步骤组成。预处理是第一步，包括通过排除严格支配的策略来减少解决方案空间。画面初始化涉及为游戏中所有相关方创建一个画面。创建完所有场景后，下一步就是旋转。通过选择进入和退出的基础变量，可以执行多次旋转迭代来为输出提供资金，这是该过程的最后一步。
数值例子
概述
一个城镇有两个出租车服务竞争对手——Beru 和 Fylt。消费者根据价格和可用性（即基于距离和乘车等待时间的乘车成本）在两家公司之间进行选择。
贝鲁的供应量较多，但历史上价格较高。Fylt 是一位想要挑战 Beru 的新人。Fylt 正在努力决定如何发展其品牌以及在哪里获得最大利润：占领那些乘坐长途、昂贵但不方便的乘车（例如去机场）的人的市场，或者为那些乘坐短途、便宜但方便的乘车的人的市场乘车，例如去杂货店。
问题陈述
Fylt 的数据分析部门分析了销售数据，并为长途和短途骑行创建了以下战略形式价格矩阵：
| 贝鲁 | |||
|---|---|---|---|
| 长距离、高（$） | 长距离、低（$） | ||
| 菲尔特 | 长距离、高（$） | 女：90，女：160 | 女：50，女：250 |
| 长距离、低（$） | 女：200，男：150 | 女：100，男：150 | |
| 贝鲁 | |||
|---|---|---|---|
| 短距离，高（$） | 短距离、低（$） | ||
| 菲尔特 | 短距离，高（$） | 女：50，男：60 | 女：10，男：30 |
| 短距离、低（$） | 女：70，男：20 | 女：50，女：30 | |
作为 Fylt 财务部门的成员，您的工作是根据数据分析部门的价格矩阵计算 Beru 和 Fylt 的主导策略。
您需要回答以下具体问题：
Beru 和/或 Fylt 是否有占优策略？如果是这样，那是什么？
如果纳什均衡存在的话，它是什么？
Fylt 应如何投资才能在更多短途或长途旅行方面超越 Beru？
解决方案
要计算主导策略，请创建 4 个图表。
图表的数量由竞争对手的数量 (2) 乘以要考虑的场景数量（价格矩阵的数量）决定。因此这个问题总共用4张图来表示。
长距离情况应有 2 个图表，短距离情况应有 2 个图表，分别为 Beru 和 Fylt。最终的图表应该是 Long-Fylt、Long-Beru、Short-Fylt、Short-Beru。
使用价格矩阵中的数据填充图表。
以 Long-Fylt 为例，根据 Fylt 选择高选项还是低选项填写 Beru 获得的值。长途价格矩阵包含本示例所需的所有值。
以 Short-Beru 为例，根据 Beru 选择高选项还是低选项填写 Fylt 获得的值。短距离价格矩阵包含本示例所需的所有值。
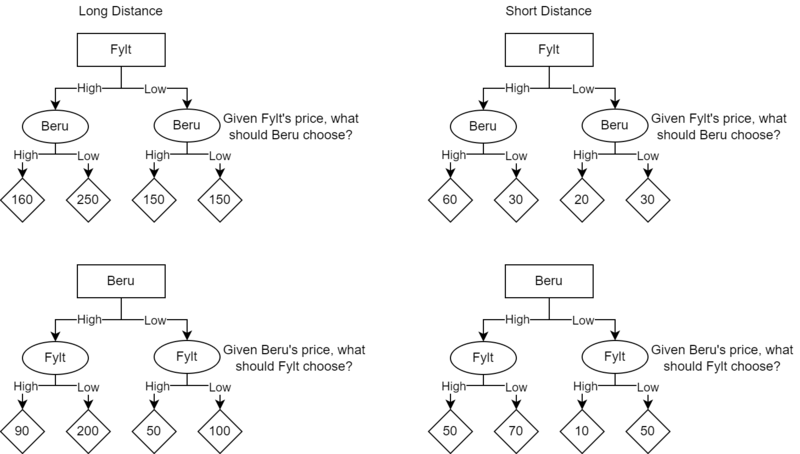帮助确定 Beru 和 Fylt 的最佳主导策略的图表。作者使用draw.io创建的图表找到 Beru 和 Fylt 在每个节点的最佳策略。
对于每个图的终端节点，圈出 Fylt 或 Beru 的最佳选择。因为我们在这个例子中最大化收益，所以最高值就是最优值
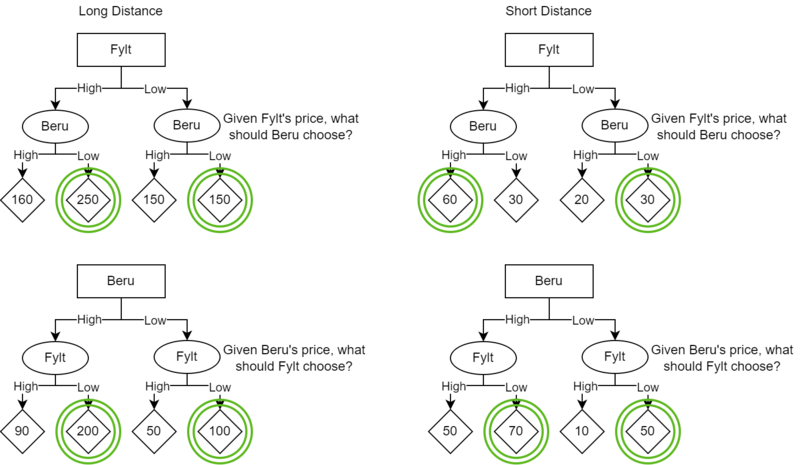演示如何根据 Fylt 和 Beru 的成本矩阵评估其策略。作者使用draw.io创建的图表确定 Beru 和 Fylt 的占优策略。
当无论竞争对手选择做什么（即价格高或低），公司总是会做出相同的选择时，就存在占优策略。
在 Long-Fylt 的例子中，如果 Fylt 的价格高，Beru 的价格就应该低；如果 Fylt 的价格较低，Beru 的价格也应该较低。因此，Beru 采取了低价定价的占优策略。
在 Short-Fylt 示例中，如果 Fylt 价格高，Beru 价格就应该高；如果 Fylt 价格低，Beru 价格也应该低。因为 Beru 的策略取决于 Fylt 的选择，所以它没有占优策略。
计算纳什均衡（如果存在）。
纳什均衡是两个竞争者所选择的最优策略。纳什均衡并不总是得到保证（即对于所有选项产生完全相同的收益并且彼此无法区分的微不足道的情况）。
通过参考上面创建的图表来确定纳什均衡。例如，对于长距离，我们看到 Beru 和 Fylt总是选择低选项作为其主导策略。对于短距离，我们注意到虽然 Fylt 没有占优策略，但 Beru却有：走低。因为Beru总是走低，那么Fylt的最佳选择也是走低。
回答最初的问题
Beru 和/或 Fylt 是否有占优策略？如果是这样，那是什么？
当距离较远时，Beru 和 Fylt 的主导策略都是设定低价。
当距离较短时，Beru 不具有占优策略，因为其最优价格取决于 Fylt 选择定价低还是高。如果 Fylt 价格较低，Beru 应该走低；但如果 Fylt 价格高，Beru 应该走高。Fylt 对于短距离有一个主导策略：低价。
如果纳什均衡存在的话，它是什么？
根据数据，短距离和长距离的纳什均衡是 Beru 和 Fylt 都设定低价。因此，对于长途旅行，Beru 为 150，Fylt 为 100。对于短途旅行，Beru 为 30，Fylt 为 50。
Fylt 应如何投资才能在更多短途或长途旅行方面超越 Beru？
Fylt 应该投资扩大其短途旅行，因为这是它比 Beru 具有利润优势的唯一领域。
应用领域
GT 的应用可以在多个学科中找到，但 GT 的总体框架允许玩家比较不同决策的结果。将讨论 GT 的流行应用程序列表，这些游戏示例可以更改并应用于广泛的场景。
游戏示例
猎鹿
这个游戏平衡了安全和社会合作。两个猎人去打猎，每个人都必须选择狩猎雄鹿或野兔，而不知道对方会选择哪一个。为了让猎人猎杀雄鹿，双方都必须猎杀雄鹿。每个人都可以单独狩猎一只野兔，但野兔的回报低于雄鹿。目标是最大化回报。[1]
性别之战
该游戏属于协调游戏类别，基于两个人在特定夜晚将做什么的决定。例如，女朋友和男朋友分别喜欢去看歌剧和足球比赛。他们在出发前不会决定要去哪里，并且全天不会互相交流。他们更喜欢自己选择的地方，但他们更愿意去同一个地方。目标是最大化幸福。[1]
囚徒困境
两名罪犯被逮捕、监禁并相互隔离。如果没有足够的证据来指控任何一个罪犯犯罪，则可能出现三种结果：两人都透露证据并都入狱四年；一人透露证据而一人保持沉默，因此揭露证据的人被释放，而沉默的人则保持沉默服刑 5 年，如果两名囚犯保持沉默，那么两人都只会在监狱里呆 2 年。目标是尽量减少入狱时间。[1]
GT 的扩展
进化博弈论
GT 是在人类互动的基础上发展起来的，但该理论被应用于生物学中，以模拟动物在竞争资源时的行为。玩家或动物不是使用逻辑，而是受繁殖成功的激励。在进化博弈论中，成功取决于竞争策略的成功频率。最终，成功的策略会被更频繁地使用，成为最后的胜利者。[1]
行为博弈论
虽然计算机可能会尝试优化效用并使用完美的逻辑，但人们发现人类并不总是使用逻辑或最大化效用。相反，行为博弈论试图建模和预测人类在游戏中的选择，而不是建议最佳解决方案。利用实验数据来显示趋势并考虑外部因素，例如情感、有限理性、文化影响和声誉等对人类在游戏中做出的决策的影响。[1]
机构设计
机制设计引入了与GT相反的方法，即目标已知，而规则和机制未知。游戏的设计必须能够激励玩家按照设计者的意图行事。举个例子，维克里拍卖风格是一种拍卖的例子，其中物品以第二高出价的价格卖给最高出价者。这种形式的游戏激励玩家诚实地评价好的事物。[1]
结论
本文总结了 GT，它是数学的一个分支，用于分析和预测具有不同数量玩家的多种不同游戏场景中的趋势。纳什均衡是 GT 中的一个基本概念，通常用作描述涉及两个或更多人的非合作博弈的例子。MILP 和 LP 都是解决 GT 中各种问题的有用编程风格。与计算纳什均衡相关的常见算法是 Lemke-Howson 算法。[4]详细介绍了基于出租车服务的数值示例，并概述了完成该示例的步骤。最后，讨论了一些利用 GT 的常见游戏示例以及 GT 的一些扩展。GT 自 1921 年以来一直存在，至今仍在应用，并将继续对所有学科的个人有用。