梁颖宗

个人信息Personal Information

教授

硕士生导师

教师拼音名称：Liang Yingzong

入职时间：2018-12-27

所在单位：材料与能源学院

联系方式：yliang@gdut.edu.cn

在职信息：在职

主要任职：Professor

其他任职：Professor

毕业院校：The Hong Kong University of Technology

学科：工程热物理

同专业硕导

教师博客

当前位置：中文主页 >> 教师博客

单纯形法

点击次数：

介绍

单纯形算法（或单纯形法）是一种广泛使用的解决线性规划（LP）优化问题的算法。单纯形算法可以被认为是解决不等式问题的基本步骤之一，因为其中许多问题将转换为 LP 并通过单纯形算法求解。^[1]单纯形算法由George Dantzig提出，其思想是逐步降级到凸多面体上的一个顶点。^[2] “单纯形”可能指的是单纯锥体的顶部顶点，它是 LP 问题中约束的几何图示。^[3]

算法讨论

LP中有两个定理：

LP问题的可行域是一个凸集（每个线性方程的二阶导数都是0，意味着趋势的单调性）。因此，如果一个LP有最优解，则必然存在可行域的一个极值点是最优的
对于LP优化问题，对于每个基本可行解，LP的可行域只有一个极值点。另外，可行域内的每一个极值点都至少有一个基本可行解。^[4]

LP问题的几何图示

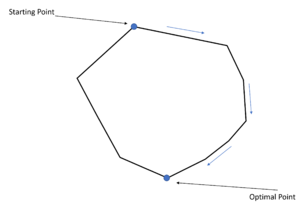
基于以上两个定理，可以描述LP问题的几何图解。该多面体的每条线将是 LP 约束的边界，根据定理，其中每个顶点将是极值点。单纯形法是调整非基本变量向不同顶点移动直至找到最优解的方法。^[5]

将以下表达式视为一般线性规划问题的标准形式：

$\max \sum _{i=1}^{n}c_{i}x_{i}$

具有以下约束：

${\begin{对齐}st\quad \sum _{j=1}^{n}a_{ij}x_{j}&\leq b_{i}\quad i=1,2,... ,m\\x_{j}&\geq 0\quad j=1,2,...,n\end{对齐}}$

单纯形法的第一步是添加表示目标函数的松弛变量和符号：

${\begin{对齐}\phi &=\sum _{i=1}^{n}c_{i}x_{i}\\z_{i}&=b_{i}-\sum _{ j=1}^{n}a_{ij}x_{j}\quad i=1,2,...,m\end{对齐}}$

新引入的松弛变量可能会与原始值混淆。因此，添加这些松弛变量会很方便 $z_{i}$ 到x变量列表的末尾，表达式如下：

${\begin{对齐}\phi &=\sum _{i=1}^{n}c_{i}x_{i}\\x_{n+i}&=b_{i}-\sum _{j=1}^{n}a_{ij}x_{ij}\quad i=1,2,...,m\end{对齐}}$

随着单纯形法的进展，起始字典（即上面的方程）在字典之间切换以寻求最优值。每个字典将有m 个构成可行区域的基本变量，以及构成目标函数的n 个非基本变量。之后，字典函数将写成以下形式：

�=�￣+Σ�=1���￣���我=乙我￣-Σ�=1��我�￣�我�我=1,2,。。。,�+米

其中带有 bar 的变量表明那些相应的值将随着单纯形法的进展而相应地变化。可以观察到，具体来说，将有一个变量从非基本变为基本，而另一个变量则相反。这种变量称为输入变量。在增加的目标下 $\phi$ ，输入变量是从集合{1,2,...,n}中选择的。只要没有重复输入变量可以选择，就会找到最优值。首先应该考虑选择哪个输入变量应该考虑到通常存在多个约束（n>1）。对于 Simplex 算法，由于主要目标是最大化，因此优先选择具有最小值的系数。

离开变量被定义为从基本变量到非基本变量。它们存在的原因是为了保证这些基本变量的非负性。一旦确定了进入变量，相应的离开变量就会发生相应的变化，如下式所示：

$x_{i}={\bar {b_{i}}}-{\bar {a_{ik}}}x_{k}\quad i\,\epsilon \,\{1,2,.. .,n+m\}$

由于要保证输入变量的非负性，因此可以得出如下不等式：

${\bar {b_{i}}}-{\bar {a_{i}}}x_{k}\geq 0\quad i\,\epsilon \,\{1,2,..., n+m\}$

在哪里 $x_{k}$ 是不可变的。最低 $x_{i}$ 应为零以获得最小值，因为它不能为负数。因此，应推导出以下方程：

$x_{k}={\frac {\bar {b_{i}}}{\bar {a_{ik}}}}$

由于所有变量的非负性， $x_{k}$ 应提高到从上述方程计算出的所有值中的最大值。因此，可以得出以下等式：

$x_{k}=\min _{{\bar {a_{ik}}}>0}\,{\frac {\bar {b_{i}}}{\bar {a_{ik}}} }\quad i=1,2,...,n+m$

一旦选择了离开基本变量和进入非基本变量，就应该进行合理的行操作，从当前字典切换到新字典，这一步称为枢轴。^[4]

与枢轴过程一样，所选枢轴元素的系数应该为 1，这意味着该系数的倒数应乘以该行中的每个元素。然后，将该特定行与相应的系数相乘，并将其添加到不同的行，对于该主元元素列中的所有其他条目，应该得到 0 值。

如果在主元过程之后还有任何负变量，则应该通过重复上述过程继续寻找主元元素。基本变量和非基本变量立即不再有负值。找到最优解。^[6]^[7]

数值例子

考虑以下数值示例以获得更好的理解：

$\max {4x_{1}+x_{2}+4x_{3}}$

具有以下限制：

${\begin{对齐}2x_{1}+x_{2}+x_{3}&\leq 2\\x_{1}+2x_{2}+3x_{3}&\leq 4\\2x_ {1}+2x_{2}+x_{3}&\leq 8\\x_{1},x_{2},x_{3}&\geq 0\end{对齐}}$

添加松弛变量可得到以下方程：

${\begin{对齐}z-4x_{1}-x_{2}-4x_{3}&=0\\2x_{1}+x_{2}+x_{3}+s_{1}& =2\\x_{1}+2x_{2}+3x_{3}+s_{2}&=4\\2x_{1}+2x_{2}+x_{3}+s_{3}&=8 \\x_{1},x_{2},x_{3},s_{1},s_{2},s_{3}&\geq 0\end{对齐}}$

单纯形表可以推导如下：

${\begin{数组}{cccccccc | r}x_{1}&x_{2}&x_{3}&s_{1}&s_{2}&s_{3}&z&b\\\hline 2&1&1&1&0&0&0&2\\1&2&3&0&1&0&0&4\\2&2&1&0&0&1&0&8\\\hline -4&-1&-4&0&0&0&1&0\end {大批}}$

在最后一行中，应选择具有最小值的列。虽然有两个最小值，但无论先选哪一个，结果都是一样的。对于此解决方案，选择第一列。找到最小系数后，通过搜索系数来进行枢轴过程 ${\frac {b_{i}}{x_{1}}}$ 。由于第一行的系数为 1，第二行的系数为 4，因此应该对第一行进行旋转。可以创建以下表格：

${\begin{数组}{cccccccc | r}x_{1}&x_{2}&x_{3}&s_{1}&s_{2}&s_{3}&z&b\\\hline 1&0.5&0.5&0.5&0&0&0&1\\1&2&3&0&1&0&0&4\\2&2&1&0&0&1&0&8\\\hline -4& -1&-4&0&0&0&1&0\end{数组}}$

通过执行行操作，第 1 列中的所有其他行（第一行除外）仍然为零：

${\begin{数组}{cccccccc | r}x_{1}&x_{2}&x_{3}&s_{1}&s_{2}&s_{3}&z&b\\\hline 1&0.5&0.5&0.5&0&0&0&1\\0&1.5&2.5&-0.5&1&0&0&3\\ 0&1&0&-1&0&1&0&6\\\hline 0&1&-2&2&0&0&1&4\end{array}}$

由于最后一行有一个负值，因此应再次执行相同的过程。最后一行中的最小值位于第三列中。在第三列中，第二行的系数最小 ${\frac {b_{i}}{x_{3}}}$ 即 1.2。因此，将选择第二行进行旋转。单纯形表如下：

${\begin{数组}{cccccccc | r}x_{1}&x_{2}&x_{3}&s_{1}&s_{2}&s_{3}&z&b\\\hline 1&0.5&0.5&0.5&0&0&0&1\\0&0.6&1&-0.2&0.4&0&0&1.2 \\0&1&0&-1&0&1&0&6\\\hline 0&1&-2&2&0&0&1&4\end{array}}$

通过执行行操作使其他列为0，可以得出以下结果

${\begin{数组}{cccccccc | r}x_{1}&x_{2}&x_{3}&s_{1}&s_{2}&s_{3}&z&b\\\hline 1&0.2&0&0.6&-0.2&0&0&0.4\\0&0.6&1&-0.2&0。 4&0&0&1.2\\0&-0.1&0&0.2&0.6&-1&0&-4.2\\\hline 0&2.2&0&1.6&0.8&0&1&6.4\end{array}}$

由于最后一行的所有值都是非负数，因此不需要进一步进行计算。从上表来看， $x_{1}$ , $x_{3}$ 和 $z$ 是基本变量，因为它们的列中的所有行都是 0，除了一行是 1。因此，最优解将是 $x_{1}=0.4$ , $x_{2}=0$ , $x_{3}=1.2$ ，达到最大值： $z=6.4$

应用

单纯形法可用于许多编程问题，因为这些问题将转换为 LP（线性规划）并通过单纯形法求解。除了数学应用之外，许多其他工业规划也会使用这种方法来最大化利润或最小化所需的资源。

数学问题

单纯形法常用于许多编程问题。由于非线性问题计算量大，许多非线性规划（NLP）问题无法有效解决。因此，许多 NLP 会依赖 LP 求解器，即单纯形法，来完成一些寻找解的工作（例如，可行解的上限或下界），或者在许多情况下，这些 NLP 将是完全线性化为 LP 并通过单纯形法求解。^[1]除了解决问题之外，单纯形法还可以可靠地用于支持其他定理的线性规划解，例如法卡斯定理，其中单纯形法证明了建议的可行解。^[1]除了解决问题之外，单纯形方法还可以启发学者解决其他问题的方法，例如二次规划（QP）。^[8]对于一些 QP 问题，它们对变量具有线性约束，可以类似于单纯形法的思想来解决。

工业应用

不同领域的行业将在约束条件下采用单纯形法进行规划。考虑到通常情况下，约束或权衡和期望结果与可控变量线性相关，许多人会开发模型通过单纯形法来解决LP问题，例如农业和经济问题

农民通常需要合理配置现有资源以获得最大利润。潜在的制约因素是从政策限制、预算问题以及耕地面积等多个角度提出的。农民可能倾向于使用基于单纯形法的模型来制定更好的计划，因为这些约束在许多情况下可能是恒定的，并且利润通常与农场产量线性相关，从而形成LP问题。目前，有一个现有的工厂模型可以接受价格、农场产量等输入，并返回最优计划，以根据给定信息实现利润最大化。^[9]

除了农业用途外，Simplex方法还可以被企业用来盈利。成功的营销实践离不开合理的营销策略。由于国际上企业众多，故选取搪瓷制品的营销策略进行说明。在广泛收集所制造的各种产品的质量、每种产品的成本以及客户受欢迎程度的数据后，公司可能需要确定哪些产品值得投资并继续盈利，哪些不值得。考虑到成本和利润因素与产量线性相关，经济学家会建议使用单纯形法求解的LP模型。^[10]

以上专业领域只是单纯形法应用的冰山一角。许多其他领域都会使用这种方法，因为 LP 问题最近越来越受欢迎，而单纯形法在解决这些问题中起着至关重要的作用。

结论

无可争议地承认单纯形方法对编程的影响，因为该方法为其发明者 George Dantzig 赢得了“国家科学奖章”。^[11]单纯形法不仅在数学模型和工业制造中具有广泛的应用，而且还为解决不等式问题提供了新的视角。因为它对规划的贡献极大地促进了当前技术和经济的进步，从限制条件下制定最优规划。如今，随着技术和经济的发展，单纯形法被一些更先进的求解器所取代，它们可以更快地解决问题，处理更多的约束和变量，但这种创新方法标志着那个时代的创造力，并不断为即将到来的挑战提供灵感。

参考

↑^{跳转至：1.0}^1.1 线性互补、线性和非线性规划网络版。
^ Dantzig，英国（1987 年 5 月）。单纯形法的起源。
^ 斯特朗，G. (1987)。卡马克算法及其在应用数学中的地位。数学情报家， 9 (2), 4-10。doi：10.1007/bf03025891。
↑^{跳转至：4.0}^4.1 范德贝，RJ (2000)。线性规划：基础和扩展。波士顿：克鲁维尔。
^ Sakarovitch M. (1983) 单纯形法的几何解释。见：Thomas JB（编辑）线性规划。施普林格电气工程文本。施普林格，纽约州，纽约州。https://doi.org/10.1007/978-1-4757-4106-3_8
^ Evar D. Nering 和 Albert W. Tucker，1993，线性规划和相关问题，学术出版社。（初级）
^ Robert J. Vanderbei，《线性规划：基础与扩展》，第 3 版，运筹学与管理科学国际系列，第 1 卷。114，施普林格出版社，2008 年。ISBN 978-0-387-74387-5。
^ 沃尔夫, P. (1959)。二次规划的单纯形法。计量经济学， 27 (3), 382.doi:10.2307/1909468
^ 华W. (1998)。修正单纯形法在农场规划模型中的应用。
^ 尼基坚科，AV (1996)。对单纯形法在设计搪瓷企业销售策略中的潜在用途进行经济分析。玻璃和陶瓷， 53 (12), 367-369。doi：10.1007/bf01129674。
^ Cottle, R.、Johnson, E. 和 Wets, R. (2007)。乔治·B·丹齐格 (1914–2005)。注意到阿米尔。数学。苏克。54、344–362。

上一条：析取规划下一条：博弈论