梁颖宗

个人信息Personal Information

教授

硕士生导师

教师拼音名称：Liang Yingzong

入职时间：2018-12-27

所在单位：材料与能源学院

联系方式：yliang@gdut.edu.cn

在职信息：在职

主要任职：Professor

其他任职：Professor

毕业院校：The Hong Kong University of Technology

学科：工程热物理

同专业硕导

教师博客

当前位置：中文主页 >> 教师博客

对偶性

点击次数：

介绍

每个优化问题都可以从原始角度或对偶角度来看待，这就是对偶原理。对偶性发展了一个优化问题与另一个相关优化问题之间的关系。如果原始优化问题是一个最大化问题，则可以使用对偶来找到其最优值的上限。如果原始问题是最小化问题，则可以使用对偶来找到下界。

根据美国数学家 George Dantzig 的说法，线性优化对偶性是 Jon von Neumann 在 Dantzig 提出线性优化问题后猜想的。冯·诺依曼确定两人零和矩阵博弈（来自博弈论）等同于线性规划。对偶理论的证明由加拿大数学家 Albert W. Tucker 和他的团队于 1948 年发表。^[1]

理论、方法论和/或算法讨论

定义

原始

max �=Σ�=1�� $z=\textstyle \sum _{j=1}^{n}\displaystyle c_{j}x_{j}$

st：

Σ�=1��我,��⪇乙我（我=1,2,。。。,米） $\textstyle \sum _{j=1}^{n}\displaystyle a_{i,j}x_{j}\lneq b_{i}\qquad (i=1,2,...,m)$

��⪈0（�=1,2,。。。,�） $x_{j}\gneq 0\qquad (j=1,2,...,n)$

双重的

min�=Σ我=1米乙我�我 $v=\textstyle \sum _{i=1}^{m}\displaystyle b_{i}y_{i}$

st：

Σ我=1米�我�我,�⪈��（�=1,2,。。。,�） $\textstyle \sum _{i=1}^{m}\displaystyle y_{i}a_{i,j}\gneq c_{j}\qquad (j=1,2,...,n)$

��⪈0（我=1,2,。。。,米） $y_{j}\gneq 0\qquad (i=1,2,...,m)$

在原始和对偶之间，变量� $c$ 和乙 $b$ 互相交换位置。系数（�� $c_{j}$ 原数的 ) 变成对偶数的右侧 (RHS)。原始的 RHS (乙� $b_{j}$ ) 成为对偶的系数。原始问题中的小于或等于约束在对偶问题中变为大于或等于。^[2]

构建双

最大限度（�时间�） �。�。��≤乙�≥0 ${\begin{矩阵}\max(c^{T}x)\\\ stAx\leq b\\x\geq 0\end{矩阵}}$ ⟶ $\quad \longrightarrow \quad$ 分钟（乙时间�） �。�。�时间�≥��≥0 ${\begin{矩阵}\min(b^{T}y)\\\ stA^{T}x\geq c\\y\geq 0\end{矩阵}}$

对偶性

如果原始问题是如上所述的最大化问题，则以下对偶性质成立。这对于弱对偶性尤其适用。

弱对偶性

让�=[�1,。。。,��] $x=[x_{1},...,x_{n}]$ 是原始问题的任何可行解
让�=[�1,。。。,�米] $y=[y_{1},...,y_{m}]$ 是对偶的任何可行解
∴ $\因此$ （x 的 z 值）≤ $\leq$ （y 的 v 值）

弱对偶定理指出，原数中 x 的 z 值始终小于或等于对偶中 y 的 v 值。

(y 的 v 值) 和 (x 的 z 值) 之间的差值称为最优对偶间隙，它始终为非负值。^[3]

强对偶引理

让�=[�1,。。。,��] $x=[x_{1},...,x_{n}]$ 是原始问题的任何可行解
让�=[�1,。。。,�米] $y=[y_{1},...,y_{m}]$ 是对偶的任何可行解
如果（x 的 z 值）= $=$ （y 的 v 值），那么x是原始的最优值，y是对偶的最优值

图解说明

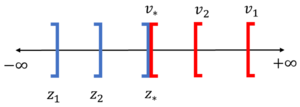
本质上，当您选择更接近最优解的 x 或 y 值时，原始的 z 值和对偶的 v 值将收敛于最优解。在数轴上，最大化的 z 值将从最优值的左侧逼近，而最小化的 v 值将从右侧逼近。

图 1：二元性的图形表示

如果原数无界，则对偶不可行
如果对偶无界，则原数不可行

强对偶定理

如果原始解有最优解�* $x^{*}$ 那么对偶问题就有最优解�* $y^{*}$ 这样

Σ�=1��*=Σ我=1米乙我�我* $\textstyle \sum _{j=1}^{n}\displaystyle c_{j}x_{j}^{*}=\textstyle \sum _{i=1}^{m}\displaystyle b_{我}y_{i}^{*}$

对偶问题及其解决方案与以下优化主题结合使用：

卡鲁什-库恩-塔克 (KKT) 变量

对偶问题的最优解是 KKT 乘数的向量。考虑我们有一个凸优化问题，其中�（�）,�1（�）,。。。,�米（�） $f(x),g_{1}(x),...,g_{m}(x)$ 是凸可微函数。假设这对（�￣,你￣） $({\bar {x}},{\bar {u}})$ 是拉格朗日函数的鞍点，�￣ ${\bar {x}}$ 和...一起你￣ ${\bar {u}}$ 满足KKT条件。该优化问题的最优解为�￣ ${\bar {x}}$ 和你￣ ${\bar {u}}$ 没有二元差距。^[4]
要具有如上所述的强对偶性，必须满足 KKT 条件。

对偶单纯形法

通过单纯形法解决线性规划问题，您可以得到其对偶的解作为副产品。这种单纯形算法试图减少对偶问题的不可行性。对偶单纯形法可以被认为是作用于对偶的变相单纯形法。对偶单纯形法是通过施加目标函数包括每个具有非正系数的变量的条件来维持对偶可行性，并在满足原始可行性条件时终止。^[5]

二元性解释

二元性可以有多种解释。以下示例包括利用对偶性的经济优化问题：

经济解释实例

一位牧场主正在准备跳蚤市场拍卖，他打算出售三种由自家羊羊毛制成的衣服：厚呢大衣、帽子和围巾。随着当地人对他的高品质服装的认可，这位牧场主计划每次在跳蚤市场开店时都将他的所有产品卖光。下面分别显示了牧场主制作短大衣、帽子和围巾的材料、时间和利润。


衣服	羊毛（英尺^2）	缝纫材料（中）	生产时间（小时）	利润（美元）
短外套	12	80	7	175
帽子	2	40	3	25
围巾	4	20	1	21

由于即将举行的跳蚤市场活动（牧场主将再次出售他的产品）的材料和时间有限，牧场主需要确定如何充分利用他的时间和材料，以最终实现利润最大化。牧场主的羊毛供应量低于平时；这周他只有 50 平方英尺的羊毛床单可以用来制作衣服。此外，牧场主只剩下 460 英寸的缝纫材料。最后，牧场主的生产服装系列的时间有限，为 25 小时。
根据上述信息，牧场主创建了以下线性程序：

最大化 �=175�1+25�2+21�3 $z=175x_{1}+25x_{2}+21x_{3}$

受：

12�1+2�2+4�3≤50 $12x_{1}+2x_{2}+4x_{3}\leq 50$

80�1+40�2+20�3≤第460章 $80x_{1}+40x_{2}+20x_{3}\leq 460$

7�1+3�2+1�3≤25 $7x_{1}+3x_{2}+1x_{3}\leq 25$

�1,�2,�3≥0 $x_{1},x_{2},x_{3}\geq 0$

在牧场主找到要生产的最佳数量的双排扣大衣、帽子和围巾之前，当地一家服装店老板走近他，询问她是否可以为她的商店购买他的劳动力和材料。由于不确定要求这些服务的合理购买价格是多少，服装店老板决定创建原始原始的双重：

最小化 �=50�1+第460章�2+25�3 $v=50y_{1}+460y_{2}+25y_{3}$

受：

12�1+80�2+7�3≥175 $12y_{1}+80y_{2}+7y_{3}\geq 175$

2�1+40�2+3�3≥25 $2y_{1}+40y_{2}+3y_{3}\geq 25$

4�1+20�2+1�3≥21 $4y_{1}+20y_{2}+1y_{3}\geq 21$

�1,�2,�3≥0 $y_{1},y_{2},y_{3}\geq 0$

通过利用上述双重因素，服装店老板能够确定牧场主的材料和劳动力的要价。在对偶中，服装店老板现在的目标是最小化要价，其中�1 $y_{1}$ 代表羊毛的数量，�2 $y_{2}$ 代表缝纫材料的数量，并且�3 $y_{3}$ 代表牧场主的劳动。

数值例子

为以下最大化问题构造对偶：

最大化 �=6�1+14�2+13�3 $z=6x_{1}+14x_{2}+13x_{3}$

受：

12�1+2�2+�3≤24 ${\tfrac {1}{2}}x_{1}+2x_{2}+x_{3}\leq 24$

�1+2�2+4�3≤60 $x_{1}+2x_{2}+4x_{3}\leq 60$

3�1+5�3≤12 $3x_{1}+5x_{3}\leq 12$

对于上面的问题，形成增广矩阵A。前两行分别表示约束一和约束二。最后一行代表目标函数。

�=[1221124305] $A={\begin{bmatrix}{\tfrac {1}{2}}&2&1\\1&2&4\\3&0&5\end{bmatrix}}$

求矩阵 A 的转置

�时间=[1213220145] $A^{T}={\begin{bmatrix}{\tfrac {1}{2}}&1&3\\2&2&0\\1&4&5\end{bmatrix}}$

从矩阵A转置的最后一行，我们可以推导出对偶的目标函数。前面的每一行代表一个约束。请注意，原始最大化问题具有三个变量和两个约束。对偶问题有两个变量和三个约束。

最小化 �=24�1+60�2+12�3 $v=24y_{1}+60y_{2}+12y_{3}$

受：

12�1+�2+3�3≥6 ${\tfrac {1}{2}}y_{1}+y_{2}+3y_{3}\geq 6$

2�1+2�2≥14 $2y_{1}+2y_{2}\geq 14$

�1+4�2+5�3≥13 $y_{1}+4y_{2}+5y_{3}\geq 13$

应用领域

对偶性出现在许多线性和非线性优化模型中。在许多此类应用中，当解决原数比较困难时，我们可以解决对偶问题。例如，如果约束多于变量(m >> n)，则解决对偶问题可能会更容易。下面将更详细地介绍和描述其中一些应用。^[6]

经济学

当计算最佳产品以产生最高利润时，可以使用对偶性。例如，原始问题可能是利润最大化，但通过对偶问题可以重新构建为成本最小化。通过将问题转化为设定原材料价格，我们可以确定所有者愿意接受的原材料价格。这些双重变量与可用资源的价值相关，通常被称为资源影子价格。^[7]

结构设计

一个例子是在结构设计模型中，梁上的张力是原始变量，节点上的位移是对偶变量。^[8]

电力网络

在对电网进行建模时，电流可以被建模为原始变量，电压差是对偶变量。^[9]

博弈论

对偶理论与博弈论密切相关。博弈论是一种用于处理多人决策问题的方法。游戏是决策问题，玩家是决策者。每个玩家选择要采取的策略或行动。当每个玩家选择策略时，每个玩家都会获得回报。冯·诺依曼猜想的零和游戏与线性规划相同，是一个玩家的收益导致另一个玩家的损失。这种零和博弈的一般情况具有与二元性类似的特征。^[10]

支持向量机

支持向量机 (SVM) 是一种流行的分类机器学习算法。SVM的概念可以分为三个部分，前两个是线性SVM，最后一个是非线性SVM。SVM 还有许多其他概念，包括超平面、函数和几何边距以及二次规划^[11]。就对偶性而言，原问题对于求解线性SVM是有帮助的，但是为了达到求解非线性SVM的目的，原问题是没有用的。这就是我们需要 Duality 来看待对偶问题来解决非线性 SVM ^[12]。

结论

自 1948 年发表对偶理论的证明以来^[1]，对偶一直是解决线性和非线性优化问题的重要技术。该理论提供了将标准极大值问题的对偶定义为标准极小值问题的思想^[2]。该技术允许优化问题一侧的每个可行解决方案为另一侧的最佳目标函数值给出界限^[6]。该技术可应用于解决经济约束、资源分配、博弈论和边界优化问题等情况。通过加深对线性程序对偶的理解，人们可以获得关于几乎任何算法或数据优化的许多重要见解。

参考

↑^{跳转至：1.0}^1.1 对偶性（优化）。（2020 年 7 月 12 日）。在维基百科中。https://en.wikipedia.org/wiki/Duality_(optimization)#:~:text=在%20mathematical%20optimization%20theory%2C%20duality中，%20primal%20(minimization )%20问题。
↑^{跳转至：2.0}^2.1 Ferguson，Thomas S.《线性规划简明介绍》。加州大学洛杉矶分校。https://www.math.ucla.edu/~tom/LP.pdf
^ 布拉德利、哈克斯和马格南蒂。（1977）。应用数学编程。艾迪生-韦斯利。http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf
^ KKT 条件和对偶性。（2018 年 2 月 18 日）。达特茅斯学院。https://math.dartmouth.edu/~m126w18/pdf/part4.pdf
^ 瓦塞克·查瓦塔尔. （1977）。对偶单纯形法。WH 弗里曼公司http://cgm.cs.mcgill.ca/~avis/courses/567/notes/ch10.pdf
↑^{跳转至：6.0}^6.1 RJ范德贝。（2008）。线性规划：基础和扩展。施普林格。http://link.springer.com/book/10.1007/978-0-387-74388-2。
^ Alaouze，CM (1996)。线性规划问题中的影子价格。 新南威尔士州 - 经济学院。https://ideas.repec.org/p/fth/nesowa/96-18.html#:~:text=In%20linear%20programming%20problems%20the,is%20increased%20by%20one%20unit。
^ 罗伯特·M·弗罗因德（2004 年，2 月 10 日）。用于约束优化的应用语言对偶性。麻省理工学院。https://ocw.mit.edu/courses/sloan-school-of-management/15-094j-systems-optimization-models-and-computation-sma-5223-spring-2004/lecture-notes/duality_article.pdf
^ 罗伯特·M·弗罗因德（2004 年 3 月）。约束优化的对偶理论。麻省理工学院。https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec18_duality_thy.pdf
^ 德里克·斯托利. （2013）。博弈论和对偶性。伊利诺伊大学厄巴纳-香槟分校。https://faculty.math.illinois.edu/~stolee/Teaching/13-482/gametheory.pdf
^ 阿布塞克·贾娜. （2020 年 4 月）。适合初学者的支持向量机 - 线性 SVM。 http://www.adeveloperdiary.com/data-science/machine-learning/support-vector-machines-for-beginners-linear-svm/
^ 阿布塞克·贾娜. （2020 年 4 月 5 日）。初学者支持向量机 - 对偶问题。 https://www.adeveloperdiary.com/data-science/machine-learning/support-vector-machines-for-beginners-duality-problem/。

上一条：博弈论下一条：线性规划