@广东工业大学 English

梁颖宗

个人信息Personal Information

副教授

硕士生导师

教师拼音名称：Liang Yingzong

入职时间：2018-12-27

所在单位：材料与能源学院

职务：Associate Professor

联系方式：yliang@gdut.edu.cn

在职信息：在职

主要任职：Associate Professor

其他任职：Associate Professor

毕业院校：The Hong Kong University of Technology

学科：工程热物理

同专业硕导

教师博客

当前位置： 中文主页 >> 教师博客

析取规划

点击次数：

介绍

析取不等式是析取约束的一种形式，可应用于线性规划。析取约束适用于所有析取编程，它只是指在线性不等式中使用逻辑约束，包括“或”、“与”或“补”语句。[1]为了求解析取，必须将约束转换为混合整数规划（MIP）或混合间线性规划（MILP）约束，这称为析取。析取涉及二元变量的实现，以创建一组可以轻松解决的新约束。析取的两种常见方法是 Big-M 重构和凸包重构。[2]

方法

一般的

当给定一组不等式时，例如{\displaystyle f_{1}(x)\leq 0\ \ \和 \ \ f_{2}(x)\leq 0}，析取形式由下式给出：  {\displaystyle {\begin{bmatrix}y\\f_{1}(x)\leq 0\end{bmatrix}}\lor {\begin{bmatrix}\neg y\\f_{2}(x)\leq 0\end{b矩阵}}.}[1]为了将问题转化为可解的 MIP 或 MILP，通过使用足够大的数来创建逻辑约束，例如{\displaystyle M_{1}}和{\displaystyle M_{2}}，以及每个不等式的二元变量 y。这如下所示{\displaystyle M},{\displaystyle y_{1}}， 和{\displaystyle y_{2}}：

{\displaystyle f_{1}(x)\leq M\ast (1-y_{1})}

{\displaystyle f_{2}(x)\leq M\ast (1-y_{2})}

要将二进制变量设置为互斥，请将变量的总和设置为 1，并将范围设置为 {0,1}。

{\displaystyle \sum _{i}y_{i}=1}

{\displaystyle y_{i}\ \epsilon \ \{0,1\}\ \ }

Big-M 重构[1] [2]

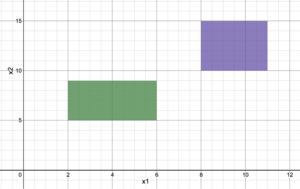图 1：可以使用 Big-M 重构或凸包重构通过析取求解的析取不等式解空间

对于 Big-M 重构，足够大的数字，{\displaystyle M}，用于取消一组约束。这是通过添加或减去术语“{\displaystyle M*(1-y)}” 分别及其各自的二元变量的上限和下限约束。虽然选择较大的 M 值可以实现隔离，但较大的值也会导致模型空间的松弛效果较差。[3]

例如，给定一个解空间{\displaystyle {\begin{bmatrix}y\\2\leq x_{1}\leq 6\\5\leq x_{2}\leq 9\end{bmatrix}}\lor {\begin{bmatrix}\neg y\\8\leq x_{1}\leq 11\\10\leq x_{2}\leq 15\ \end{bmatrix}}}（如图 1 所示），为了确定哪个解决方案是最佳的，必须制定问题以选择一组约束。使用 Big-M 重构，将获得以下 MILP 集：

{\displaystyle y}公式

{\displaystyle 2-M*(1-y_{1})\leq x1\leq 6+M*(1-y_{1})}

{\displaystyle 5-M*(1-y_{1})\leq x2\leq 9+M*(1-y_{1})}

{\displaystyle \neg y}公式

{\displaystyle 8-M*(1-y_{2})\leq x1\leq 11+M*(1-y_{2})}

{\displaystyle 10-M*(1-y_{2})\leq x2\leq 15+M*(1-y_{2})}

凸包重构[1] [2]

与 Big-M 重构类似，凸包重构使用二元变量 y 来约束不等式集。将问题转化为可解 MILP 的第一步是将所有变量分解为一组变量，例如（{\displaystyle x_{1}}→{\displaystyle x_{11}}+{\displaystyle x_{12}}）。通过添加这些附加变量，可以隔离哪些参数集提供了问题的最佳解决方案。然后，与Big-M重构类似，使用足够大的变量M来消除非最优变量集，例如{\displaystyle x_{11}}和{\displaystyle x_{12}}。对于图 1 所示的问题，将制定以下变量约束：

{\displaystyle y}公式

{\displaystyle 0\leq x_{11}\leq M*y_{1}}

{\displaystyle 0\leq x_{21}\leq M*y_{1}}

{\displaystyle \neg y}公式

{\displaystyle 0\leq x_{12}\leq M*y_{2}}

{\displaystyle 0\leq x_{22}\leq M*y_{2}}

然后将实施数值约束的制定：

{\displaystyle y}公式

{\displaystyle 2\ast y_{1}\leq \ x_{11}\ \leq 6\ast y_{1}}

{\displaystyle 5\ast y_{1}\leq \ x_{21}\ \leq 9\ast y_{1}}

{\displaystyle \neg y}公式

{\displaystyle 8\ast y_{2}\leq \ x_{12}\ \leq 11\ast y_{2}}

{\displaystyle 10\ast y_{2}\leq \ x_{22}\ \leq 15\ast y_{2}}

通过凸包变换，额外的约束限制了问题，因此与 Big-M 公式相比，可以检查更紧密的（凸）解空间。[3]

数值例子

给定下面的析取不等式形式，使用凸包方法和 Big-M 重新表述以下问题：

{\displaystyle {\begin{bmatrix}y\\0\leq x_{1}\leq 13\\0\leq x_{2}\leq 4\\1\leq x_{2}+x_{3}\leq 7\end{bmatrix}}\lor {\begin{bmatrix}\neg y\\2\leq x_{1}\leq 10\\4\leq x_{2}\leq 6\ \\2\leq x_{ 2}+x_{3}\leq 8\end{b矩阵}}}

凸包法

我们首先设置引入一个二元变量 y 作为总和为 1：

{\displaystyle y_{1}+y_{2}=1,y_{1},y_{2}\epsilon }{0,1}

接下来我们开始对我们的{\displaystyle x_{ij}}价值观。

{\displaystyle x_{1}=x_{11}+x_{12}}

{\displaystyle x_{2}=x_{21}+x_{22}}

{\displaystyle x_{3}=x_{31}+x_{32}}

接下来用另一个二元变量large取消非最优变量集{\displaystyle M}变量为：

{\displaystyle 0\leq x_{11}\leq y_{1}*M}

{\displaystyle 0\leq x_{21}\leq y_{1}*M}

{\displaystyle 0\leq x_{31}\leq y_{1}*M}

{\displaystyle 0\leq x_{12}\leq y_{2}*M}

{\displaystyle 0\leq x_{22}\leq y_{2}*M}

{\displaystyle 0\leq x_{32}\leq y_{2}*M}

请记住{\displaystyle M}必须足够大，太大的值会导致 LP 弛豫不良。

最后，根据原始约束重新制定以下约束，重新制定为{\displaystyle y}包含在引脚中{\displaystyle x_{ij}=0}什么时候{\displaystyle y_{j}=0}，受原始约束，当{\displaystyle y_{j}=1}。

{\displaystyle 0\leq x_{11}\leq y_{1}*13}

{\displaystyle 0\leq x_{21}\leq y_{1}*4}

{\displaystyle 1*y_{1}\leq x_{21}+x_{31}\leq y_{1}*7}

{\displaystyle 2*y_{2}\leq x_{12}\leq y_{2}*10}

{\displaystyle 4*y_{2}\leq x_{22}\leq y_{2}*6}

{\displaystyle 2*y_{2}\leq x_{22}+x_{32}\leq y_{2}*8}

因此，重新表述的约束集是所有这些约束，使问题成为 MIP。

大M法

我们现在提出用 Big-M 方法重新表述的相同约束集。我们可以从设置 2 个二进制变量开始{\displaystyle y_{1}}和{\displaystyle y_{2}}总和为 1。

{\displaystyle y_{1}+y_{2}=1,y_{1},y_{2}\epsilon }{0,1}

接下来，我们添加二进制变量{\displaystyle M}因为它是一个任意大的常数，用于重新表述不等式。每个不等式都是通过加或减一步形成的{\displaystyle M*(1-y_{i})}取决于不等式是大于或等于，还是小于或等于。

{\displaystyle -M*(1-y_{1})+0\leq x_{1}\leq 13+M(1-y_{1})}

{\displaystyle -M*(1-y_{1})+0\leq x_{2}\leq 4+M(1-y_{1})}

{\displaystyle -M*(1-y_{1})+1\leq x_{2}+x_{3}\leq 7+M(1-y_{1})}

{\displaystyle -M*(1-y_{2})+2\leq x_{1}\leq 10+M(1-y_{2})}

{\displaystyle -M*(1-y_{2})+4\leq x_{2}\leq 6+M(1-y_{2})}

{\displaystyle -M*(1-y_{2})+2\leq x_{2}+x_{3}\leq 8+M(1-y_{2})}

这样，如果{\displaystyle y_{1}=1}和{\displaystyle y_{2}=0}第一组不平等被强制执行，第二组不平等被急剧扩大，有效地阻止它们限制问题，因为{\displaystyle M}足够大。

应用领域

图2：废水系统

析取不等式规划可用于解决各个领域的现实问题。利用多个约束所依赖的二元决策变量的整数规划公式可以重新公式化为析取不等式公式。

带状包装问题

条带堆积问题是一个众所周知的问题，其中二维矩形或条带在二维网格中对齐，但受到条带不重叠的约束。表述此问题的一种方法是将非重叠约束描述为一组四个语句： 对于现有矩形{\displaystyle A}，一个新的矩形{\displaystyle B}必须位于矩形的上方、下方、左侧或右侧{\displaystyle A}。每种情况都代表一个独特的不平等约束；例如，如果{\displaystyle B}上面是{\displaystyle A}，那么它的下边界必须成立{\displaystyle B}的值大于下边界{\displaystyle A}加上高度{\displaystyle A}。这可以扩展到消除对称性并提高解决方案的效率[4]。这也可以扩展到三个维度，用于装载货船等应用。

流程调度

当可能存在多个设置、反应器或过程时，析取不等式对于过程工程中的决策非常有价值。在流程调度中，机器和车间操作的调度方式是为了最大化最终产品的产量、最小化停机时间或最大化利润。这些操作背后的许多决策都是二元的：是否在给定时间运行机器/操作。如果机器/操作正在运行，则需要约束来定义与正在运行的机器/操作相关的成本（资本支出和运营成本）、利润、热力学约束和资源（包括质量和能量平衡）。如果机器/操作未运行，则需要一组不同的约束来定义闲置成本和资源。这可以表述为析取不等式公式并使用所描述的方法求解。析取不等式的形式为：

{\displaystyle MinZ=f(x)+\textstyle \sum _{k\epsilon K}c_{k}\displaystyle }

{\displaystyle stg(x)\leq 0}

{\displaystyle {\underset {i\epsilon D_{i}}{\lor }}{\begin{bmatrix}Y_{ki}\\r_{ki}(x)\leq 0\\c_{k}=l_ {ki}\end{bmatrix}}k\epsilon K}

{\displaystyle \veebar _{i\epsilon D_{i}}Y_{ki}}

在这个一般公式中，{\displaystyle c_{k}}代表执行一项条款的成本，连续变量代表系统参数，约束代表热力学和资源约束，如上所述[5]。一些具体应用包括蒸馏塔、制药纯化厂和废水处理厂。

图 2 显示了流程调度的一个特例，即从混合物中去除污染物的废水网络。任务是计算出排放污染的总成本。[6]该废水系统可以重新表述为非凸一般析取规划问题，如下所示：[6]

{\displaystyle MinZ=\textstyle \sum _{k\epsilon PU}CP_{k}\displaystyle }

{\displaystyle f_{k}^{j}=\textstyle \sum _{i\epsilon M_{k}}f_{i}^{j}\displaystyle } {\displaystyle \forall jk\in MU}

{\displaystyle \textstyle \sum _{i\epsilon S_{k}}f_{i}^{j}\displaystyle =f_{k}^{j}} {\displaystyle \forall jk\in SU}

{\displaystyle \textstyle \sum _{i\epsilon S_{k}}\zeta _{i}^{j}\displaystyle =1} {\displaystyle k\in SU}

{\displaystyle f_{k}^{j}=\textstyle \zeta _{i}^{k}f_{k}^{j}\forall _{j}\displaystyle } {\displaystyle i\in S_{k}} {\displaystyle k\in SU}


{\displaystyle {\underset {h\epsilon D_{k}}{\lor }}{\begin{bmatrix}y\\f_{i}^{j}=\mathrm {B} _{i}^{jh },i\epsilon OPU_{k},i^{i}\epsilon IPU_{k},\forall _{j}\\F_{k}=\sum _{j}f_{i}^{j}, i\epsilon OPU_{k}\\CP_{k}=\partial _{ik}F_{k}\end{bmatrix}}k\epsilon PU}


{\displaystyle 0\leq \zeta _{i}^{k}\leq 1} {\displaystyle \forall j,k}

{\displaystyle 0\leq f_{i}^{j},f_{k}^{j}} {\displaystyle \forall i,j,k}

{\displaystyle 0\leq CP_{k}} {\displaystyle \forall k}

{\displaystyle YP_{k}^{h}\in }{真假}{\displaystyle \forall h\in D_{k}\forall k\in PU}

结论

如图所示，析取不等式可用于制定各种不同类型的混合整数程序线性和非线性程序，其中二元决策确定约束集。用于重新表述问题的两种方法是凸包和 Big-M 重新表述。可以证明，要获得 0 或 1 混合整数程序的凸包，一次取每个 0 或 1 变量的凸包就足够了[3]。实施 Big-M 方法可生成更小的 MILP/MINLP，并且比凸包方法具有更严格的松弛，从而提供更高效的计算解决方案。正如 Balas 和 Bonami [7]的研究所示，析取不等式还可以用于提高任何通用分支和切割算法的性能。许多可以通过析取不等式解决的现实世界问题都涉及过程优化，其中必须做出各种二元决策来优化解决方案。这里展示的现实世界问题的例子包括货物包装和加工厂，例如废水处理厂。总之，用析取不等式来表述这些类型的问题可以简单地表示并转换为 MILP/MILP，并可以使用标准 MILP/MINLP 求解算法来求解。

参考

  1. ↑跳转至：1.0 1.1 1.2 1.3 E. Balas，“析取编程”，Discr 年鉴。数学，卷。5，第 6-11 页，1979 年。

  2. ↑跳转至：2.0 2.1 2.2 佩德罗·M·卡斯特罗和伊格纳西奥·E·格罗斯曼。“广义析取编程作为导出调度公式的系统建模框架。” 2012 51 (16), 5781-5792 DOI: 10.1021/ie2030486

  3. ↑跳转至：3.0 3.1 3.2 你，风起。（2021）。“混合整数线性规划。”

  4. ^ 弗朗西斯科·特雷斯帕拉西奥斯和伊格纳西奥·格罗斯曼。“带状堆积问题的广义析取规划公式的对称性破缺。” 运筹学年鉴 258，第 1 期 2（2017）：747-759。

  5. ^ 格罗斯曼、伊格纳西奥·E.和弗朗西斯科·特雷斯帕拉西奥斯。“通过广义析取规划对离散连续优化模型进行系统建模。” AIChE 期刊 59，第 1 期 9（2013）：3276-3295。

  6. ↑跳转至：6.0 6.1 格罗斯曼、伊格纳西奥 E. 和胡安 P. 鲁伊斯。广义析取规划：MINLP 优化的公式化和替代算法的框架，混合整数非线性规划，Springer 纽约，2012 年。

  7. ^ E.巴拉斯，P.博纳米。“从 LP 单纯形表生成提升和投影削减：新变体的开源实现和测试。Math.Prog.Comp.1”，165–199 (2009)

广东工业大学网络信息与现代教育技术中心电话：020-39323866   版权所有@ 2020-2021保留所有权利  
粤ICP备05008833号
手机版 访问量：次

开通时间： ..

最后更新时间： ..